De harmonische rij kun je doorzetten tot n. Definieer
\(H(n)=\sum_{k=1}^{n}\frac{1}{k}\).
\(H(n)\) divergeert logaritmisch: \(H(n)\approx\log(n)\) als n groot wordt. De vraag is waarom.
Nu is het zo dat de integraal \(\int_1^{n}\frac{1}{x}dx\) benaderd kan worden door een Riemann-som.
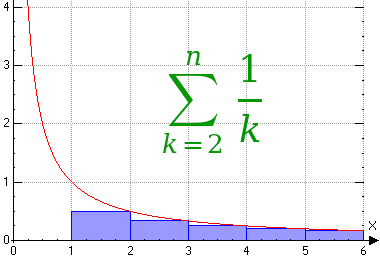
Een ondersom:

En een bovensom:
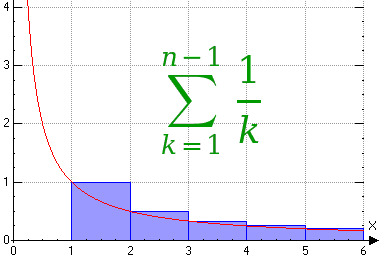
De grafiek van \(\frac{1}{x}\) daalt op het interval \([1,n]\), dus:
\(\sum_{k=2}^n\frac{1}{k}<\int_1^n\frac{1}{x}dx<\sum_{k=1}^{n-1}\frac{1}{k}\). Werk je de integraal uit en trek je \(H(n)\) van alle drie af, dan krijg je:
\(\sum_{k=2}^n\frac{1}{k}-H(n)<\log(n)-H(n)<\sum_{k=1}^{n-1}\frac{1}{k}-H(n)\).
\(-\frac{1}{1}<\log(n)-H(n)<-\frac{1}{n}\). Vermenigvuldig alles met -1. De tekens klappen om:
\(\frac{1}{n}<H(n)-\log(n)<1\).
Het verschil tussen de harmonische rij en de natuurlijke logaritme zit dus altijd tussen de 0 en de 1: De harmonische rij divergeert logaritmisch.